Why do I descend faster the further I get down a pitch?
Something I have often noticed while descending pitches in caves is that the further down the pitch/rope I get the faster I am travelling. So I set about using some of my kinematics knowledge to analyse the system and see what is going on.
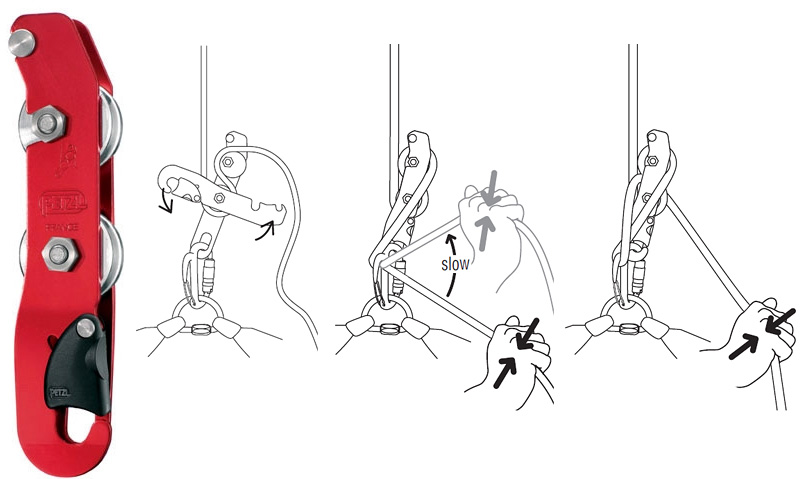
Simple, with diagram showing friction points where the rope is in contact with the Simple & braking carabiner
Firstly I wrote out some potential reasons for this observation.
- The rope is perhaps wetter at the bottom, this can be very common when caving in Ireland as our caves tend to be damp.
- The further down you go the less (free hanging) rope there is below you.
GIF showing the caver of mass M in descent
After some thought that concluded that the second reason was the most probable. So I looked to the Capstan Equation $\eqref{eq:capstan}$. Where $\mu$ is the coefficient of friction and $\beta$ is the angle swept out by the rope’s point of contact with the bobbin/carabiner.
[ T_{2} = T_{1}e^{\mu \beta} \label{eq:capstan} \tag{1} ]
Since each bobbin and carabiner would add it’s own amount of friction / tension to the rope I wrote out three equations $\eqref{eq:group}$, with $T_0$ being the tension in the rope initially, $T_1$ is the tension in the rope after contact with the first bobbin, $T_2$ after contact with the second bobbin etc. Where $T_{0} \gt T_{1} \gt T_{2} \gt T_{3}$.
[ \begin{aligned} T_{1} &= T_{0}e^{\mu_{a} \beta_{1}} \nonumber \newline T_{2} &= T_{1}e^{\mu_{a} \beta_{2}} \nonumber \newline T_{3} &= T_{2}e^{\mu_{s} \beta_{3}} \nonumber \end{aligned}\label{eq:group} \tag{2} ]
Looking at the capstan equation each friction point adds a certain amount of friction regardless of where on the rope the caver is, i.e. friction is independent of position. But that is not to say tension is independent of position. In fact I think that the initial tension $T_0$ must be equal to the combined mass of the caver and free hanging rope times $g$ (See Equation $\eqref{eq:3}$). The mass of the free hanging rope below the caver is a function of, $x$, the caver’s distance from the pitch head, as $x$ increases $m$ decreases.
[ T_{0} = (M + m(x))g \label{eq:3} \tag{3} ]